파이썬 그래프 탐색 알고리즘(BFS, DFS)

그래프 탐색 알고리즘

시작 정점에서 간선을 타고 이동할 수 있는 모든 정점을 찾는 알고리즘

그래프 탐색 알고리즘에는 깊이우선탐색과 너비우선탐색이 있다.

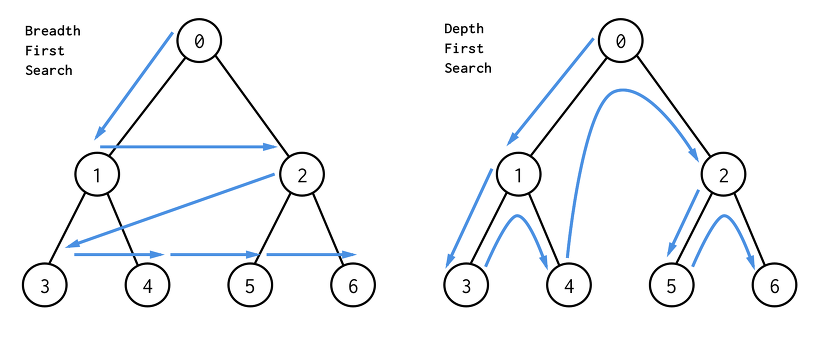
깊이우선탐색(Depth-First Search, DFS)

스택 + 그래프

그래프의 깊이를 우선으로 탐색하기 위해 스택의 개념 사용

너비우선탐색(Breadth-First Search, BFS)

그래프 + 큐

그래프의 너비를 우선으로 탐색하기 위해 큐의 개념 사용

깊이우선탐색(Depth-First Search, DFS)

시작 정점으로부터 갈 수 있는 하위 정점까지 가장 깊게 탐색하고, 더 이상 갈 곳이 없다면 마지막 갈림길로 돌아와서 다른 정점을 탐색하며 결국 모든 정점을 방문하는 순회 방법

깊이우선탐색을 미로 탈출로 생각하면 이해하기 쉽다.

어느 한 쪽 길로 가장 깊게 들어갔다가 막히면 다시 돌아와서 다른 길을 탐색한다.

깊이우선탐색의 특징

• 모든 정점을 방문할때 유리하다. 따라서 경우의 수, 순열과 조합 문제에서 많이 사용한다.

• 너비우선탐색에 비해 코드 구현이 간단하다.

• 단, 모든 정점을 방문할 필요가 없거나 최단 거리를 구하는 경우에는 너비우선탐색이 유리하다.

1. DFS를 하기 전에, 일단 탐색을 진행할 그래프가 필요하다.

2. 그래프는 인접 행렬 혹은 인접 리스트 방식으로 표현할 수 있다.

3. 각 정점을 방문했는지 여부를 판별할 방문 체크 리스트가 필요하다.

4. 사람과 달리 컴퓨터는 각 정점에 방문했는지 알 수 없으므로 visited 리스트를 따로 선언하여 각 정점을 방문했는지 체크한다.

visited = [False] * n # n은 정점의 개수

인덱스는 각 정점의 번호

방문한 정점은 True, 방문하지 않은 정점은 False

[DFS의 사이클]

1. 현재 정점 방문처리
2. 인접한 모든 정점 확인
3. 방문하지 않은 인접 정점 이동

graph = {
  [1, 2],
  [0, 3, 4],
  [0, 4, 5],
  [1],
  [1, 2, 6],
  [2],
  [4]
}

visited = [False] * n # 방문 처리 리스트 만들기

stack = [start] # 돌아갈 곳을 기록
visited[start] = True # 시작 정점 방문 처리

while len(stack) != 0: # 스택이 빌 때 까지(돌아갈 곳이 없을때까지)반복
  cur = stack.pop() # 현재 방문 정점(후입 선출)
  
  for adj in graph[cur]: # 인접한 모든 정점에 대해
    if not visited[adj]: # 아직 방문하지 않았다면
      visited[adj] = True # 방문 처리
      stack.append(adj) # 스택에 쌓기
      
  """
  for adj in [1, 2]:
  	if not visited[1]:
  		visited[adj] = True
  		stack.append(adj)
  """

DFS는 직전에 방문한 정점으로 차례로 돌아가야 하므로, 후입선출(LIFO) 구조의 스택을 사용한다.