파이썬 그래프(graph)
2022, Aug 09
그래프(graph)
그래프의 개념
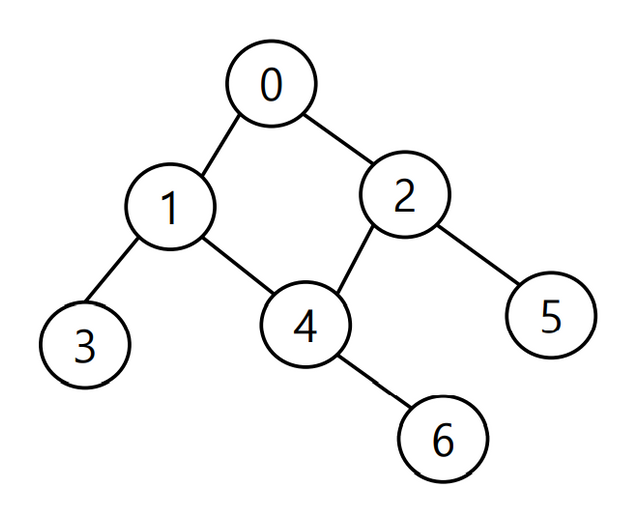
정점(Vertex)과 이를 연결하는 간선(Edge)들의 집합으로 이루어진 비선형 자료구조
- 정점, 노드(Vertex, Node) : 간선으로 연결되는 객체
- 간선(Edge) : 정점 간의 연결 관계를 표현하는 선
- 경로(Path) : 시작 정점부터 도착 정점까지 거치는 정점을 나열한 것
- 인접(Adjacency) : 두 개의 정점이 하나의 간선으로 직접 연결된 상태
그래프의 종류
무방향 그래프 (Undirected graph)
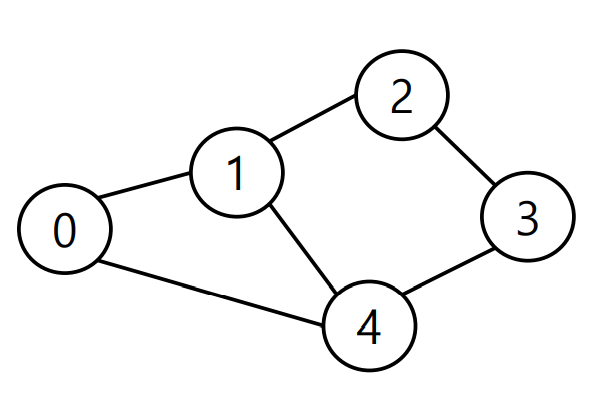
- 간선의 방향이 없는 가장 일반적인 그래프
- 간선을 통해 양방향의 정점 이동 가능
- 차수(Degree) : 하나의 정점에 연결된 간선의 개수
- 모든 정점의 차수의 합 = 간선 수 x 2
방향 그래프 (Directed graph)
- 간선의 방향이 있는 그래프
- 간선의 방향이 가리키는 정점으로만 이동 가능
- 차수(Degree) : 진입 차수와 진출 차수로 나누어짐
- 진입 차수(In-degree) : 외부 정점에서 한 정점으로 들어오는 간선의 수
- 진출 차수(Out-degree) : 한 정점에서 외부 정점으로 나가는 간선의 수
그래프의 표현
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다.
다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다.
어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다.
입력으로 주어지는 간선은 양뱡향이다.
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다.
V부터 방문된 점을 순서대로 출력하면 된다.
| 입력 | 출력 |
|---|---|
4 5 1 1 2 1 3 1 4 2 4 3 4 |
1 2 4 3 1 2 3 4 |
- 문제에서는 그래프를 위와 같이 간선이 연결하는 두 정점의 목록으로 제공
인접 행렬(Adjacent matrix)
- 두 정점을 연결하는 간선이 없으면 0, 있으면 1을 가지는 행렬로 표현하는 방식
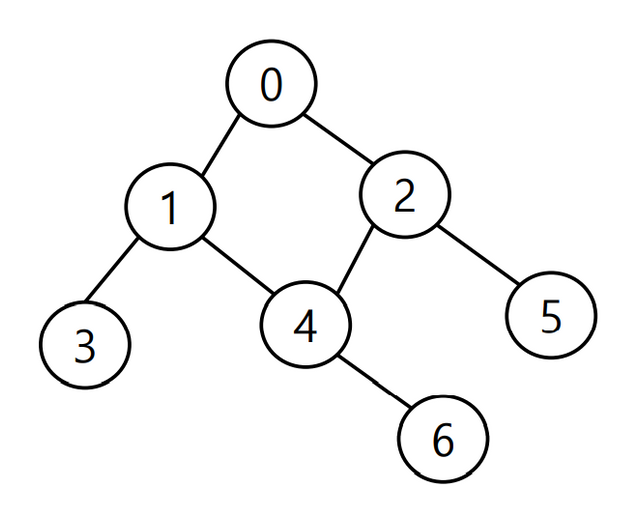
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 5 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
# 인접 행렬 만들기
from pprint import pprint
# N 정점 개수 M 간선 개수
N, M = map(int, input().split())
# N 크기만큼의 인접행렬을 생성
matrix = [[0] * N for _ in range(N)]
edges = [] # 간선의 시작점, 끝점을 담을 리스트
for _ in range(M):
# 간선의 시작점, 끝점
u, v = map(int, input().split())
edges.append([u, v]) # [1, 2] [2, 5] [5, 1] [3, 4] [4, 6]
for edge in edges:
# v1 = 1 / v2 = 2
v1, v2 = edge[0], edge[1] # 리스트에 담긴 간선의 시작점[0], 간선의 끝점[1]을 각각 담는다
# 좌우 대칭으로 입력
matrix[v2][v1] = 1 # matrix[2][1]
matrix[v1][v2] = 1 # matrix[1][2]
pprint(matrix)
#[[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 0, 0, 1, 0],
# [0, 1, 0, 0, 0, 1, 0],
# [0, 0, 0, 0, 1, 0, 0],
# [0, 0, 0, 1, 0, 0, 1],
# [0, 1, 1, 0, 0, 0, 0],
# [0, 0, 0, 0, 1, 0, 0]]
# 유방향 인접행렬
from pprint import pprint
N, M = map(int, input().split())
matrix = [[0] * N for _ in range(N)]
edges = []
set_edgs = set()
for i in range(M):
u, v = map(int, input().split())
edges.append([u, v])
for edge in edges:
v1, v2 = edge[0], edge[1]
matrix[v1][v2] = 1
pprint(matrix)
#[[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 1, 0],
# [0, 0, 0, 0, 1, 0, 0],
# [0, 0, 0, 0, 0, 0, 1],
# [0, 1, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]]
- 인접 행렬은 직관적이고 만들기 편하지만, 불필요하게 공간이 낭비됨
인접 리스트(Adjacent list)
- 리스트를 통해 각 정점에 대한 인접 정점들을 순차적으로 표현하는 방식
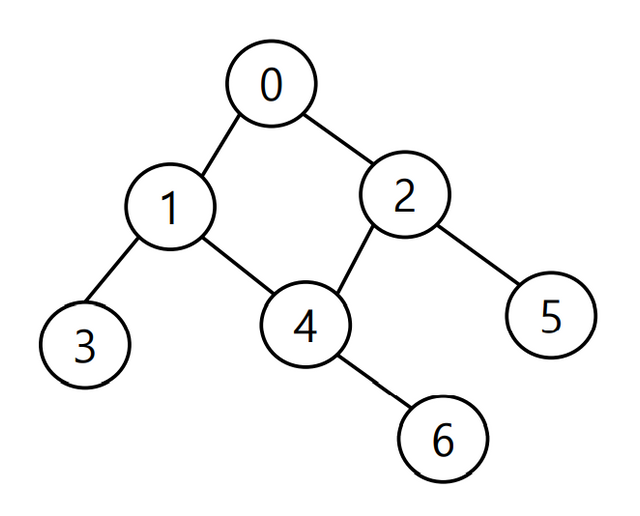
| 0 | 1 | 2 | |
|---|---|---|---|
| 1 | 0 | 3 | 4 |
| 2 | 0 | 4 | 5 |
| 3 | 1 | ||
| 4 | 1 | 2 | 6 |
| 5 | 2 | ||
| 6 | 4 |
# 인접 리스트 만들기
# N 정점 개수 M 간선 개수
N, M = map(int, input().split())
# N길이의 빈 2중 리스트 생성
adj_list = [[] for _ in range(N)]
# M길이만큼 반복하며
for _ in range(M):
# 간선의 시작점(u), 간선의 끝점(v) 추가
u, v = map(int, input().split()) # 1, 2 / 2, 5 / 5, 1 / 3, 4 / 4, 6
# 연결된 값 끼리 추가해준다.
adj_list[v].append(u) # adj_list[2].append(1)
adj_list[u].append(v) # adj_list[1].append(2)
# 인접 리스트 결과
print(adj_list)
# [[], [2, 5], [1, 5], [4], [3, 6], [2, 1], [4]]
# 유방향 인접 리스트
N, M = map(int, input().split())
adj_list = [[] for _ in range(N)]
for i in range(M):
u, v = map(int, input().split())
adj_list[u].append(v)
print(adj_list)
# [[], [2], [5], [4], [6], [1], []]
인접 행렬 vs 인접 리스트
인접 행렬은 직관적이고 만들기 편하지만, 불필요하게 공간이 낭비된다.
인접 리스트는 연결된 정점만 저장하여 효율적으로 자주 사용된다.